Video: Hur bevisar man att diagonalerna på en romb delar varandra?
2024 Författare: Lynn Donovan | [email protected]. Senast ändrad: 2023-12-15 23:53
I en romb alla sidor är lika och motsatta sidor är parallella. Vidare a romb är också ett parallellgram och uppvisar därför egenskaper av a parallellogram och det diagonaler i ett parallellogram delar varandra.
På motsvarande sätt delar diagonalerna på en romb varandra?
I någon romb , den diagonaler (linjer som länkar samman motsatta hörn) dela varandra i räta vinklar (90°). Det är, varje diagonal skär av Övrig i två lika delar, och vinkeln där de korsar är alltid 90 grader. I figuren ovan drar du valfri vertex för att omforma romb och övertyga dig själv att det är så.
För det andra, är rombdiagonalerna vinkelräta? Egenskaper för en Romb De diagonaler är vinkelrät till och dela varandra. Intilliggande vinklar är kompletterande (till exempel ∠A + ∠B = 180°). A romb är en parallellogram vars diagonaler är vinkelrät till varandra.
Med tanke på detta, hur bevisar man att diagonalerna på en romb är vinkelräta bisektrar?
Bevis Att den diagonalerna på en romb är vinkelräta Fortsättning på ovan bevis : Motsvarande delar av kongruenta trianglar är kongruenta, så alla 4 vinklarna (de i mitten) är kongruenta. Detta leder till det faktum att de alla är lika med 90 grader, och diagonaler är vinkelrät till varandra.
Är romb ett parallellogram?
DEFINITION: A romb är en parallellogram med fyra kongruenta sidor. SAT: Om a parallellogram är en romb , delar varje diagonal ett par motsatta vinklar. SAT Omvänt: Om en parallellogram har diagonaler som delar ett par motsatta vinklar, det är en romb.
Rekommenderad:
Hur delar jag upp ett Word-dokument i två lika stora delar?
Word 2016 & 2013: Dela sida i kolumner Markera texten du vill dela upp i kolumner. Välj fliken "Sidlayout". Välj "Kolumner" och välj sedan den typ av kolumner du vill använda. Ett. Två. Tre. Vänster. Höger
Vilken komponent är mest sannolikt att tillåta fysiska och virtuella maskiner att kommunicera med varandra?
Vilken komponent kommer troligen att tillåta fysiska och virtuella maskiner att kommunicera med varandra? -Virtuella switchar tillåter flera virtuella servrar och/eller stationära datorer att kommunicera på ett virtuellt nätverkssegment och/eller fysiskt nätverk. Virtuella switchar konfigureras ofta i hypervisorn
Vilka parallellogram har diagonaler som delar varandra?
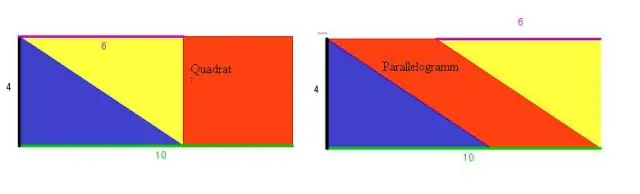
Om två intilliggande sidor av ett parallellogram är lika, så är det en romb. Detta test tas ofta som definitionen av en romb. En fyrhörning vars diagonaler delar varandra i räta vinklar är en romb
Hur bevisar man en linjär kod?
En linjär kod definieras vanligtvis som ett delrum till Fn för något fält F (eftersom du pratar om bitar kan du ta F=F2={0,1}). Koden C som genereras av en genererande matris G är spännvidden av raderna i G. Spännvidden för en uppsättning vektorer i Fn är ett delrum till Fn, så C är en linjär kod
Hur bevisar man stark induktion?
Den starka induktionsprincipen säger att man kan bevisa ett påstående av formen: P(n) för varje positivt heltal n. enligt följande: Basfall: P(1) är sant. Starkt induktivt steg: Antag att k är ett positivt heltal så att P(1),P(2),,P(k) alla är sanna. Bevisa att P(k + 1) är sant